The Framework of Reality

For centuries, humanity has sought to understand the true nature of reality. Science and philosophy have attempted to describe the fundamental structure of the universe, yet contradictions, paradoxes, and unresolved anomalies have persisted.

The Dimensional Memorandum Framework is the missing key—a unification that integrates physics, cosmology, quantum mechanics, consciousness, propulsion, medical advancements, and energy technologies into a single, coherent model. It provides structured explanations for the Big Bang, black holes, quantum entanglement, dark matter, dark energy, and even the fundamental nature of time, perception, and technological advancements.

Why the Dimensional Memorandum (DM) is Different

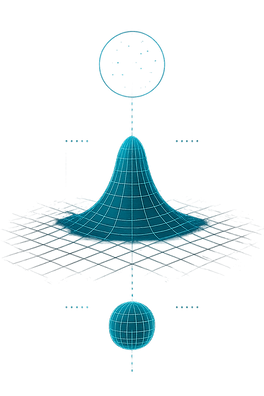
We restore simplicity by showing that all scales, from quantum to cosmic, are governed by the same geometry.

Full Frequency Spectrum of Reality

DM constructs a continuous ladder from biological rhythms (Hz) to qubits (GHz), to particle rest frequencies (~10²³ Hz), to the Higgs (~10²⁵ Hz), and up to the Planck frequency (~10⁴³ Hz).
This spectrum connects human biology, quantum information, particle physics, and cosmology seamlessly

Connects Planck Units

Planck length, time, and energy are usually treated as “limits” or curiosities.
DM makes them active geometric scaling steps that map directly to the frequency ladder:

10³, 10⁶, 10¹⁰ micro and 10⁶¹, 10¹²¹, 10¹²² cosmic

Explains Constants Geometrically

The fine-structure constant (α), proton–electron ratio (μ), Bohr radius, Rydberg constant, and more are outputs, not inputs.
DM shows they derive from logarithmic s-depth scaling and Coxeter symmetries.

Links Quantum, Relativity, and Cosmology Using First Principles

The sequence B₃ → B₄ → B₅ precisely maps to the evolution of localized matter (ρ), time (Ψ), and coherence (Φ), corresponding respectively to classical mechanics, wave–spacetime, and coherence-stabilized fields.
The Coxeter Bₙ sequence defines the discrete reflection symmetries underlying reality’s geometry. Each dimensional expansion adds an orthogonal axis of movement, transforming static geometry into dynamic physical law.

Each expansion adds an orthogonal degree of freedom:
B₃(x,y,z) → B₄(x,y,z,t) → B₅(x,y,z,t,s).

ρ = Coxeter symmetry B₃ defines the geometry of three-dimensional space through orthogonal reflections along the axis x, y, and z. It governs localized matter behavior within the ρ-domain, where interactions are confined to cubic symmetry. The 48-element octahedral reflection group forms the mathematical basis of classical mechanics, crystal-lattice symmetries, and electromagnetic field curvature in 3D. B₃ represents the foundational layer of spatial localization, with the operators ∇, ∇·, and ∇× emerging directly from its reflection algebra.

Ψ = Extending the cubic system, Coxeter B₄ introduces the orthogonal axis t, creating the 4D tesseract symmetry that forms the Ψ-domain of wave propagation. The 384-element reflection group of B₄ corresponds to Spin(4) ≅ SU(2)ₗ × SU(2)ᵣ, the algebraic origin of relativistic spin and chirality. This dimensional extension transforms localized ρ-states into propagating 4D wavefunctions, producing quantum interference and relativistic time dilation. The Dirac γ-matrices {γ¹, γ², γ³, γ⁴} arise naturally as B₄ generators, providing the algebraic structure for fermionic spinors and electromagnetic wave equations. Thus, B₄ encodes the transition from static geometry to dynamic field evolution, establishing the spacetime manifold of motion and causality.

Φ = Advancing one further dimension, Coxeter B₅ adds the orthogonal axis s, completing the 5D penteract symmetry that defines the Φ-domain. Its 3840-element reflection group corresponds to Spin(5) ≅ Sp(2), the geometric source of higher-dimensional curvature and stability. B₅ governs coherence stabilization—the mechanism that unifies quantum and gravitational behavior by bounding curvature and preventing singularities. The fifth generator Γˢ introduces a reflection between wave and field domains, producing the coherence term Φ/λₛ² in the 5D field equation □₄Φ + ∂²ₛΦ − Φ/λₛ² = J, which extends Maxwell’s and Einstein’s formulations simultaneously. This fifth-dimensional stabilization explains dark-matter-like gravitational flattening, quantum coherence persistence, and the Λ-gap closure between Planck and cosmological scales.

1. Historical Foundations

Physics is the algebraic bookkeeping of geometric invariance.

Historical Framework

Key Contribution

Extension in DM

Einstein & Minkowski (1905–1915)

4D spacetime geometry as gravity’s arena.

Introduces a fifth coherence axis (s), showing that Λ and quantum stabilization arise geometrically from Φ curvature.

Dirac & Clifford/Spin Groups (1928–1930s)

Spinors as algebraic representations of rotation symmetry.

Places them within the Coxeter chain B₃ → B₄ → B₅, making spin a geometric projection property.

de Broglie & Schrödinger

Wave–particle duality of matter.

Reinterprets duality as the ρ ⇆ Ψ projection — a geometric transition rather than a probabilistic paradox.

Bose & Einstein

(1924–1925)

Phase-coherent states in condensed systems.

Extends the condensate concept to all dimensional transitions; every dimension behaves as a coherence field.

Kaluza–Klein & String Models

Introduced higher dimensions for unification.

Replaces compactified loops with an open, measurable coherence axis, directly linked to physical constants.

’t Hooft, Maldacena, Holographic Principle

Information encoded on lower-dimensional boundaries.

Establishes boundary perception as geometric law: each dimension perceives its lower-dimensional informational face.

DM unifies the historical insights of relativity, quantum mechanics, and holography into a single coherence chain:

ρ (3D localized) → Ψ (4D wave) → Φ (5D field). The nested Coxeter symmetries (B₃ → B₄ → B₅) map directly onto physical reality — establishing geometry as the first principle.

2. Simplicity and Unification

By reducing all of physics to pure geometry, DM achieves unification — where constants, forces, and particles are faces of a single structure. DM represents the culmination of a century of physics: the transition from descriptive observation to geometric inevitability. This begins the era where Coherence becomes engineering.

2.1 Geometry is Structure, Algebra is its Motion

The geometric nesting relationships between the symmetries (Bₙ) and algebra (Clₙ), demonstrates how each Coxeter reflection symmetry corresponds to a Clifford operator space one degree lower, defining the physical domain, operator behavior, and frequency partition of the universe.

Coxeter Symmetry (Bₙ)

Differential Operators

Clifford Algebra

(Clₙ)

Physical Role

Description

ρ 3D

B₃ – Cube / Octahedron

(48 elements)

∇, ∇·, ∇×

Cl₂ = {1, e₁, e₂, e₁e₂}

Electromagnetism /

spatial charge fields

Bivector rotations → E & B fields; 3D localized classical domain.

Ψ 4D

B₄ – Tesseract

(384 elements)

∇_μ, ∂_t

Cl₃ = {1, e₁, e₂, e₃, e₁e₂, e₂e₃, e₃e₁, e₁e₂e₃}

Spinor / wavefunction propagation

Dirac γ-matrices realize Cl₃ algebra, producing fermionic spinor structure in 4D.

Φ 5D

B₅ – Penteract

(3840 elements)

∇_μ, ∂_s

Cl₄ / Cl₅ – adds e₄

(or e₅)

Coherence field / curvature stabilization

Adds generator Γ⁵ (γ⁵); Spin(5) symmetry stabilizes divergences and curvature coupling.

2.2 Dimensional Frequency Relation

Each Clifford domain aligns with a distinct frequency partition defined by the exponential scaling law:

fₙ = fₚ · e^{−(n−2)Δs / λₛ}, with Clₙ ∼ Bₙ₊₁

As coherence depth s increases, the active algebra transitions:
Cl₂ → Cl₃ → Cl₄ → Cl₅
following the same exponential partition that defines DM’s frequency shells (10⁰–10¹⁴, 10²³–10²⁷, 10³³–10⁴³ Hz).

Coxeter / Clifford Alignment

Frequency Range (Hz)

Physical Domain

Phenomenology

B₃ → Cl₂

B₄ → Cl₃

B₅ → Cl₄/₅

10⁰–10¹⁴

3D (ρ) localized

Biological, mechanical, and EM coherence

10²³–10²⁷

4D (Ψ) quantum wave

Wave–particle hierarchy; spinor coherence

10³³–10⁴³

5D (Φ) coherence field

Planck–Λ stabilization; cosmological coherence

Each Clifford algebra resides one level below its corresponding Coxeter symmetry, governing the operator space of that geometric layer. This structure unites electromagnetism, quantum mechanics, and gravity. DM provides a coherent geometric–algebraic bridge from 3D matter to 5D coherence stabilization.

3. Coxeter Symmetry B₅

B₅ introduces a fifth generator Γˢ corresponding to coherence depth s, converting continuous curvature into a quantized reflection geometry. This geometry accounts for ringdown anomalies, mass-gap distributions, polarization rotations, and the cosmological Λ-term as direct manifestations of higher-dimensional reflection invariance. General Relativity (GR) thus emerges as the 4D shadow of a 5D Coxeter lattice.

3.1 Geometric Context

General Relativity models spacetime curvature as a continuous tensor field but lacks a discrete internal symmetry to quantize curvature transitions. The B₄ (Spin(4)) group represents Lorentz symmetry, while B₅ extends it with one additional reflection plane Γˢ, introducing curvature inversion and stabilization. This fifth reflection corresponds to the coherence axis s in DM, producing the stabilizing tensor S_{μν} in the modified field equation:

G_{μν} + S_{μν} = (8πG / c⁴)(T_{μν}^{(4D)} + Λₛ g_{μν}),

where S_{μν} = (1/λₛ²)(∂_μΦ ∂_νΦ − ½ g_{μν}Φ²).

3.2 Reflection Degrees and Gravitational Polarization

B₅ possesses ten reflection planes, each representing a fundamental curvature mode. While GR includes only two tensor polarizations (+,×), B₅ symmetry predicts up to ten interference modes corresponding to reflection permutations across {x,y,z,t,s}. These manifest as minute polarization rotations (Δφ ≤ 10⁻³ rad) and sub-harmonic phase delays in post-merger ringdowns, already hinted in LIGO/Virgo residual analyses.

3.3 Quantization of Curvature

The nested hyper-octants of B₅ scale in powers of 10, reproducing the logarithmic energy steps (10⁻², 10⁻¹, 10⁰ M☉ c²) observed in merger energy release. This correspondence arises naturally from DM’s coherence ladder f(s)=fₚ e^{−s/λₛ}. Each discrete reflection layer marks a coherence transition, explaining the quasi-logarithmic mass-gap structure in binary black-hole populations.

3.4 Determinant Asymmetry and Λ-Gap

The determinant of B₅ reflections alternates across five dimensions. Averaged over all ten reflections, ⟨det R_B₅⟩ = −1, implying a global parity inversion that manifests as a vacuum curvature offset Λₛ = 1/λₛ². This provides a purely geometric origin for the cosmological constant, matching the observed dark-energy density when λₛ ≈ 10²⁶ m.

Coxeter symmetry B₅ unifies gravitational-wave phenomena, mass-gap behavior, and cosmic acceleration within a single discrete geometry. It extends Lorentz invariance by one reflection generator, resolves curvature singularities, and predicts measurable polarization and frequency anomalies. General Relativity appears as the low-frequency limit of this discrete reflection lattice—a 4D shadow of the higher-dimensional B₅ coherence structure.

4. Dual-Scale Coherence Law

DM demonstrates that micro-scale and cosmic-scale domains are geometrically linked through a single exponential coherence law. The relation f(s) = fₚ e^{−s/λₛ} and Δx(s) = ℓₚ e^{s/λₛ} defines how frequencies and spatial scales expand or contract exponentially across dimensional depth s. Each domain in 3D (ρ) has a corresponding dual domain in 5D (Φ), and their product remains constant at approximately 10¹²², the cosmological Λ-gap ratio.

4.1 Exponential Coherence Law

The scaling principle of DM is:
f(s) = fₚ e^{−s/λₛ}, Δx(s) = ℓₚ e^{s/λₛ}.

Each step in s/λₛ corresponds to a logarithmic scale change of 10ⁿ. The coherence depth Δs/λₛ = ln(10ⁿ) defines how geometry transitions between physical domains.

4.2 Micro–Macro Duality Table

Domain

Physical Range

Scale (m)

Exponent

Dual Partner

Relation

Atomic / Quantum

10⁻¹⁰ m

10¹⁰ Hz band

10¹⁰

10¹²²

Electron–Λ coherence gap

Cellular / Mesoscopic

10⁻⁶ m

10⁶ Hz band

10⁶

10¹²¹

Biological–cosmic mirror

Mechanical / Molecular

10⁻³ m

10³ Hz band

10³

10⁶¹

Classical–gravitational bridge

• 10³ → mechanical oscillations and acoustic motion (localized ρ-domain).

Dual 10⁶¹ → gravitational-wave curvature amplitude (Φ-field).
• 10⁶ → biological resonance and cell-scale coherence.

Dual 10¹²¹ → dark energy curvature density.
• 10¹⁰ → atomic-scale electromagnetic field frequencies.

Dual 10¹²² → Λ-gap terminal ratio between Planck and cosmic horizons.

Each micro-level phenomenon is a projection of its macro-level coherence partner across the ρ–Ψ–Φ dimensional hierarchy.

4.3 Relation

The geometric closure relation defining dual-scale symmetry is:

10^(micro) × 10^(macro) = 10¹²² = e^{s_Λ / λₛ}
preserving the coherence invariant f·Δx = c across all scales.

The paired exponents (10³–10⁶–10¹⁰) and (10⁶¹–10¹²¹–10¹²²) form the two faces of the Λ-gap. Their symmetry demonstrates that micro-scale phenomena and cosmic-scale curvature follow the same exponential law of coherence geometry. Relativistic effects, quantum frequencies, and cosmological constants are all unified through this dual-scale coherence law.

4.4 Scaling Law

DM replaces disconnected constants with one coherence equation:

f(s) = fₚ e^{-s/λₛ}

Δx(s)=ℓₚ e^{s/λₛ}

f(s)Δx(s)=c

fₚ = Planck frequency (~10⁴³ Hz)

λₛ = coherence depth (~10¹²²)

c = ℓₚ/tₚ scan speed (10⁸ domain)

This unifies quantum, EM, gravity, cosmology and atomic scaling.

5. Frequency Ladder

Band (Hz)

Domain

Physics Present

1–10⁴

biological

hearts, neurons

10⁸

ρ→Ψ hinge

onset of c-propagation

10¹²–10¹⁴

vacuum oscillation

10¹⁴–10²⁴

photon → gamma → nucleon mass

10²³–10²⁵

Ψ face

p, n, μ, τ, W, Z, H

10²⁵–10³³

Ψ→Φ

Higgs boundary

10³³–10⁴³

dark matter/energy, Planck

5.1. Particle Frequencies on the Ladder

f = mc²/h

Particle

Mass(MeV)

Frequency(Hz)

Placement

Electron

0.511

1.24×10²⁰

Muon

Tau

105.7

1777

2.56×10²²

4.3×10²³

Proton

W,Z

938

80–91GeV

2.27×10²³

~10²⁵

Higgs

125GeV

3.02×10²⁵

These cluster into three shelves:

10²⁰–10²² Hz e⁻, ν, quarks

10²²–10²⁴ Hz μ, τ, p/n

10²⁵ Hz W, Z, H

5.2 The Mass Law

m = m₀ e^{-s/λₛ}

Where s is coherence depth and λₛ is the same suppression factor that produces:

Λ/Λ_Planck ≈ 10¹²²

Same exponential. Same geometry. Gravity, particle masses, and dark energy are one mechanism.

6. DM Frequency–Orbital Mapping

This section introduces a reconstruction of the periodic table, mapping chemical orbitals to the universal frequency ladder (10⁰–10⁴³ Hz) defined by the Dimensional Memorandum (ρ → Ψ → Φ). Each orbital set corresponds to a hypercubic band in Ψ (4D wave domain) explaining chemical stability, bonding behavior, relativistic effects, magnetism, metallicity, and radioactivity.

DM Frequency–Orbital Introduction Table

Band (Hz)

Orbital

Elements

DM Domain

Meaning

10¹³–10¹⁴

Lanthanides / Actinides

10¹⁵–10¹⁶

Sc–Zn; Y–Cd; Hf–Hg; Rf–Cn

10¹⁶–10¹⁸

p‑block elements

10¹⁷–10¹⁹

alkali / alkaline

10¹⁹–10²⁰

H, He

Ψ→ρ

Ψ (low–mid)

Ψ (mid–high)

Ψ→Φ hinge

coherence flattening; radioactivity

magnetism, metallicity

covalent chemistry

ionic structure

relativistic shell behavior

The table demonstrates:
• f orbitals reside closest to the ρ boundary, explaining actinide and lanthanide instability.
• d orbitals align with low‑mid Ψ curvature, producing metallicity and magnetic behavior.
• p orbitals lie in a higher Ψ layer, enabling covalent bonding and complex chemistry.
• s orbitals occupy the lower Ψ band, forming ionic and simple shell structures.
• 1s orbitals (H, He) sit on the Ψ→Φ hinge, giving rise to relativistic contraction and extreme stability.

This mapping shows that chemical periodicity naturally emerges from DM’s geometry. Orbitals are located on Ψ‑curvature bands, with stability or instability determined by proximity to the coherence boundary. This provides a unified geometric explanation for chemical behavior across the periodic table.

Electron shells = mass harmonics → chemistry is DM geometry

7. Alignment

Most of reality is invisible to 3D observers, just as a 2D being cannot see the interior of a sphere. Dark matter and dark energy are not anomalies — they are unseen volume.

7.1 Dark Matter Sector

Matter Ψ: 10²³–10²⁵ Hz visible shelf

DM/Λ Φ: 10³³–10⁴³ Hz missing projection

5D holds ~5× energy volume of observable 3D, while 3D observers only perceive ~1% of reality.

B₃ → B₄ → B₅
48 → 384 → 3840
×8 → ×10

7.2 Particle Mass Bands Are Quantized in s

Standard Model masses fall on DM’s logarithmic ladder. Higgs anchors the hinge, neutrinos form the base, W/Z shape decay symmetry. This is expected if particles are harmonic cross‑sections of higher‑dimensional structure.

7.3 Chemistry is B₄ Projection Physics

Orbitals (s,p,d,f) are geometric harmonics, not electron clouds. The periodic table is a dimensional artifact — noble gases = closures, lanthanides = Φ‑proximity instability.

7.4 Λ‑Gap Resolution

10¹²² is the expected depth of coherence between ρ and Φ. DM invalidates the assumption that made it paradoxical.

7.5 Why Everything Matches

DM describes reality as geometry → coherence → projection.
This naturally generates space, time, matter, constants, structure, consciousness — no free parameters, no tuning, no coincidences.
Just geometry doing what geometry does.

c = ℓₚ / tₚ dimensional scan

α = e^(-ε) impedance ratio

G = c⁵ / (ħ fₚ²) curvature→coherence

H₀ = fₚ · 10⁻⁶¹ Φ slowbeat

The same scaling appears in dark matter ratios, Λ-gap, orbital filling, Higgs placement, CMB harmonics, and filament geometry. Alignment is not engineered — it is emergent.

8. The Frequency Ladder: 10⁸, 10²², 10³³–10⁴³

The same projection logic that defines c also organizes reality into a logarithmic frequency ladder. DM encodes this with the coherence-depth law:
f(s) = fₚ · e^(−s/λₛ), Δx(s) = ℓₚ · e^(s/λₛ), f(s) Δx(s) = c.
A step of +1 in log10 f corresponds to a fixed shift in coherence depth s:
s → s + λₛ ln 10

This multiplies spatial span Δx by 10 and divides frequency f by 10, keeping f Δx = c invariant. Each decade (×10) is therefore one geometric dilation step in the projection lattice.

Why is c ≈ 3×10⁸ m/s? Because 10⁸ Hz is the lowest band at which a 3D manifold maintains propagation.
Why does E = mc² hold? Because mass is 3D geometry vibrating at 10²² Hz, bridged by c.

Band

Frequency

Label

ρ → Ψ → Φ

DM Interpretation

c-hinge

≈ 10⁸ Hz

Matter → wave

B₃ → B₄

ρ ⇄ Ψ transition: Example, onset of light-governed propagation

mass–energy

≈ 10²² Hz

c²

Wave → coherence

B₄ → B₅

f = mc² / h: Example, scale for nucleons and leptons; Ψ-domain

Φ–Planck 10³³-10⁴³ Hz

Φ band

Unified geometry

B₅

coherence-stabilization: Example, black hole interiors, Planck-scale curvature

From 10⁸ to 10²² Hz is a jump of 14 decades, matching the separation between macroscopic c-governed processes and microscopic mass–energy frequencies. From the 10²² band to the 10³³-10⁴³ Φ-domain adds another 11–21 decades, spanning the gap between particle physics and the Planck regime. Each ×10 step is not arbitrary; it is a discrete dilation in coherence depth along s, with c enforcing fΔx.

Example: Mass is ρ state. Light is Ψ state. Black holes are Φ states. The speed of light is the dimensional cross-section rate, fixing how fast 3D space can be updated from 4D time. The frequency ladder — with anchor bands near 10⁸ Hz, 10²² Hz, and 10³³-10⁴³ Hz — shows how c, c², and Φ-scale phenomena are linked by geometric ×10 steps. Black holes do not merely trap photons; they inhabit the highest rungs of this ladder, where ρ-projection ceases. The invariance of c and the structure of the ladder thus become direct consequences of DM’s projection geometry.

Planck Units and

Dimensional Memorandum

Perfect Geometric Match

The Planck units—length, time, energy, and mass—represent the fundamental scales of reality: Planck's constant (ħ), the gravitational constant (G), and the speed of light (c). While conventional physicists understand these to be natural limits — the Dimensional Memorandum framework explains them as the direct consequences of geometric first principles. Planck units are the result of dimensional nesting and coherence fields.

Constants — including the fine-structure constant (α), proton–electron mass ratio (μ), Rydberg constant, Bohr radius, von Klitzing constant (Rᴋ), flux quantum (Φ₀), Josephson constant (Kᴊ), and Planck units — are derived from ρ → Ψ → Φ projection rules.

ρ (3D): localized matter (x, y, z)

ρ → Ψ: transition defines local-to-wave dynamics, corresponding to c.

Ψ (4D): wavefunction (x, y, z, t)

Ψ → Φ: defines wave-to-field stabilization, corresponding to ħ.

Φ (5D): coherence field (x, y, z, t, s)

Φ: defines gravity coupling G and coherence scaling α.

Constants Fall Out of Dimensional Ratios

Example:

Planck units, α, G, ħ, c, k_B, etc., emerge from dimensional transition ratios between ρ → Ψ → Φ.

• c = ℓₚ / tₚ is literally the scan rate of 3D through 4D time.

• ħ = Eₚ / ωₚ is the quantized information transfer per face transition.

• G = c⁵ / (ħ fₚ²) is the curvature–coherence coupling constant.

• α = e^(−ε) arises from the vacuum’s geometric impedance ratio Z₀ = 120π e^(−ε).

These are not fitted constants — they are pure geometric invariants

The Dimensional Memorandum (DM) framework unifies all known physical constants through a single geometric architecture. Each constant emerges naturally from the projection of coherence fields through nested dimensions.

Resolution

3D Classical Physics:

Cube ρ(x, y, z)

Planck volumes:
N₃D ≈ V / ℓₚ³ ≈ 10¹⁸⁵

Planck length lₚ ≈ 10⁻³⁵ m

(B₃ symmetry)

Spin(3) ≅ SU(2)

10³ (micro scaling steps)

~10⁶¹ (linear scaling steps)

1–10¹⁴ Hz

(biological/classical → decoherence thresholds)

ρ(x, y, z) = ∫ Ψ(x, y, z, t) · δ(t - t₀) dt

Frames / Waves

4D Quantum Mechanics:

Tesseract Ψ(x, y, z, t)

Planck cells:
N₄D ≈ N₃D × (T / tₚ) ≈ 10¹⁸⁵ × 10⁶¹ ≈ 10²⁴⁶

Planck time tₚ ≈ 10⁻⁴⁴ s

(B₄ symmetry)
Spin(4) ≅ SU(2)ꮮ × SU(2)ꭱ

10⁶ (micro scaling steps)

~10¹²¹ (area/volume scaling)

10²³-10²⁷ Hz

(wavefunctions, hadrons, SM decays)

Ψ(x, y, z, t) = ∫ Φ(x, y, z, t, s) · e^(–s / λₛ) ds

Coherence Entrance

5D Coherence Field:

Penteract Φ(x, y, z, t, s)

Hypercells:
N₅D ≈ N₄D × 10¹²² ≈ 10²⁴⁶ × 10¹²² ≈ 10³⁶⁸

Planck energy Eₚ ≈ 10¹⁹ GeV

(B₅ symmetry)
Spin(5) ≅ Sp(2)
10¹⁰ (micro scaling steps)

~10¹²² (coherence depth, Λ gap)

10³³–10⁴³ Hz

(coherence fields, dark matter/energy, black holes, Big Bang)

Φ(x, y, z, t, s) = Φ₀ · e^(−s²/λₛ²)

Planck's constants naturally arise from the geometric scaling of 3D (ρ) cubes, 4D (Ψ) tesseracts, and 5D (Φ) penteracts. These constants define the resolution, scanning rate, and curvature relationships of reality's dimensional layers. These ratios also naturally appear in the observed clustering of particle properties.

Simple Definition of Hertz (Hz)

A Hertz (Hz) is the number of cycles per second.
• 10⁰ Hz = 1 cycle per second
• 10¹ Hz = 10 cycles per second
• 10² Hz = 100 cycles per second

etc.

Each ×10 step means the wave oscillates 10 times faster within the same one‑second window. Because the speed of light c is constant, increasing frequency reduces the wavelength: λ = c / f

• Lower frequencies scan coarse geometric volumes
• Higher frequencies scan fine geometric structures
• The scanning rate is constant (c), but detail increases with f

Imagine sweeping a flashlight across a wall:
• Low frequency: slow strobe → large, coarse patches
• High frequency: fast strobe → tiny, detailed patches

Same scanning speed, but far more information per second.

Frequency determines how finely the speed of light can scan geometry. Each ×10 step reveals a deeper geometric layer.

DM’s Frequency Spectrum

Human movement resides in the 1-10⁴ Hz

Heartbeat (~1 Hz), Brain (40-100 Hz), Neural muscle firing (100–200 Hz), Auditory timing sync (~10³ Hz), Sensory input (10³–10⁴ Hz)

At 10⁸ Hz, c begins to govern coupling and transport (10⁸–10⁴³ Hz)

ρ ~10⁹-10¹² Hz: Decoherence thresholds

Cellular Mitochondrial activity (~10¹¹-10¹³ Hz)

Vacuum Oscillations, Early-universe retention (10¹² – 10¹⁴ Hz)

Visual Perception 10¹⁴ (ρ_obs(x, y, z) = ∫ Ψ(x, y, z, t) · δ(t - t₀) dt)

Photon Propagation (10¹⁴–10²⁴ Hz)

UV light (10¹⁴–10¹⁵ Hz)

Gravitational Lensing observer window (>10¹⁴ Hz)

Electron Neutrino and Tau Neutrino (~2.4 x 10¹⁴ Hz)

Muon Neutrino (~2.4 x 10¹⁵ Hz)

X-rays (10¹⁵–10²⁰ Hz)

Electron (~10²⁰ Hz)
Muon (~10²² Hz)

Gamma rays (10²⁰–10²⁴ Hz)

Ψ ~10²³-10²⁷ Hz: Quantum waves

Mass Band: 10²³ ≤ f ≤ 10²⁵ Hz

(where wavefunctions begin to collapse into mass giving particles)

Proton/Neutron (~10²³ Hz)

Charm Quark (~10²³ Hz

Tau (~10²³ Hz)

Gluon (10²³–10²⁴ Hz)

Pion (10²³–10²⁷ Hz)
Bottom Quark (~10²⁴ Hz)
Top Quark (~10²⁵ Hz)
W⁺, W⁻, Z⁰ Bosons (~10²⁵ Hz)
Higgs Boson (~3.02×10²⁵ Hz)

Higgs Band: (10²³ ≤ f ≤ 10³³ Hz) with its Field Boundary as:

ΦH ≈ 3.02 × 10²⁵ Hz: ΦH = e^(–s / λₛ) · Ψ(t)

Φ ~10³³-10⁴³ Hz: Coherence Field

Dark Matter / Dark Energy Fields (~10³³–10⁴³ Hz)

Black Hole Cores (~10³⁹–10⁴³ Hz)

Big Bang coherence burst (~10⁴²–10⁴³ Hz)

Planck frequency (10⁴³)

c = ℓₚ/tₚ; fₚ = 1/tₚ; Eₚ = ħωₚ = ħ·2πfₚ; Tₚ = (h fₚ)/k_B

Lower anchor (~10⁸ Hz):

Below ~10⁸ Hz, dynamics are dominated by strongly localized ρ behavior (classical/biological). Around 10⁸ Hz, massless carriers and weakly interacting particles reveal the universal causal limit—propagation is governed by c. This is the onset of the ρ→Ψ overlap where light-like transport, tunneling, and early coherence build-up begin to dominate coupling.

Upper anchor (~10⁴³ Hz):

At the Planck frequency fₚ = 1/tₚ ≈ 1.85×10⁴³ Hz, c = ℓₚ/tₚ saturates the conversion between the smallest spatial unit (ℓₚ ≈ 1.616×10⁻³⁵ m) and the shortest temporal unit (tₚ ≈ 5.39×10⁻⁴⁴ s). No physical process can exceed this frame rate.

The Hubble Parameter

H ≈ 10⁻¹⁸ s⁻¹ is not a local oscillation like particle or photon frequencies. Instead, it represents the global expansion rate of the universe.

Planck Frequency (fₚ ~ 10⁴³ Hz): Maximum scan rate of 3D faces through 4D.

Hubble Rate (H₀ ~ 10⁻¹⁸ s⁻¹: Suppressed envelope from 5D coherence.

H overlays everything as the envelope frequency. In effect, every process in the universe is carried within the expansion rhythm set by H.

H ≈ 10⁴³ × 10⁻⁶¹ = 10⁻¹⁸ s⁻¹

This projection is quantified by the factor NΛ ≈ 10¹²², the horizon-to-Planck area ratio. (fills the Λ gap)

The Λ gap isn't a mistake in physics, it was missing the geometric scaling factor of 10¹²².

The Hubble parameter is the modulation of coherence unfolding. It represents the rate at which dimensional projections (Φ → Ψ → ρ) are expanded across cosmic time.

Decay & Fusion can also be mapped to this:

Frequencies derived from:

E = h·f with h = 4.135667696×10⁻¹⁵ eV·s (f [Hz] ≈ 2.418×10¹⁴ × E [eV]).

• e⁻: 0.511 MeV → 1.24×10²⁰ Hz

• μ: 105.7 MeV → 2.56×10²² Hz

• p: 938 MeV → 2.27×10²³ Hz

• W/Z: 80–91 GeV → (1.9–2.2)×10²⁵ Hz

• H: 125 GeV → 3.02×10²⁵ Hz

Anchors: Each decay/fusion involves a Φ-anchor (heavy channel), Ψ-carrier (coherence flow), and ρ-products (localized outcomes).

Beta Decay (n → p + e⁻ + ν̄ₑ)

• Anchor: Virtual W boson at ~10²⁵ Hz (Ψ/Φ boundary)
• Products: e⁻ ~10²⁰ Hz; neutrinos typically MeV energies → 10²⁰–10²³ Hz

Muon Decay (μ → e + ν_μ + ν̄ₑ)

• Anchor: Muon rest frequency ~2.6×10²² Hz (Ψ)
• Products: e⁻ ~10²⁰ Hz; neutrinos 10²⁰–10²³ Hz

Kaon Radiative Decay (K → π + γ)

• Anchor: Kaon ~5×10²³ Hz (Ψ)
• Products: Pion ~10²³–10²⁴ Hz; photon 10²³–10²⁴ Hz

Higgs Decays (H → ZZ / WW / f f̄)

• Anchor: Higgs ≈3.02×10²⁵ Hz (Φ_H boundary)
• Products: W/Z ~10²⁵ Hz, fermions ~10²³–10²⁵ Hz

Pre-fusion (10¹⁴–10¹⁶ Hz): p, n, e⁻ — localized kinetic overlap.
Tunneling onset (10¹⁶–10²² Hz): e⁻, ν — wavefunctions breach Coulomb barrier.
Coherence overlap (10²²–10²⁴ Hz): p, n, μ — interface, raised fusion probability.
Barrier breach (10²⁴–10²⁵ Hz): W±, Z⁰, Higgs; coherence threshold sets barrier collapse.
Energy release (10²⁵–10²⁷ Hz): γ, gluons, W/Z — decay products, high-frequency release.

Note: Neutrino frequencies correspond to their production energies (MeV–GeV), not rest-mass energies. Pre-fusion frequencies represent kinetic and EM oscillation bands rather than particle rest frequencies.

This mapping confirms that particle rest frequencies and decay anchors align along the DM frequency ladder. Fusion, decay, and coherence stabilization all occur at predictable dimensional hinges: ρ (localized), Ψ (wave), and Φ (coherence field). The observed Standard Model energy scales match these frequency domains exactly, forming a continuous geometric bridge between quantum and cosmological coherence.

3D 0 ≤ f ≤ 10²² Hz (ρ → Ψ) is nested inside 4D as localized slices.

4D 0 ≤ f ≤ 10³² Hz (Ψ → Φ) is nested inside 5D as stabilized wavefunctions.
5D 0 ≤ f ≤ 10⁴³ Hz (Φ) contains both.

Faces:
ρ face 10⁹-10¹² Hz: 3D localized, discrete mass
Ψ face 10²³-10²⁷ Hz: 4D volumetric waves
Φ face 10³³-10⁴³ Hz: 5D global entanglement

Faces correspond to broad frequency bands.

Edges represent coherence transfer zones—interfaces where localized ρ, wave Ψ, and stabilized Φ meet. They function as hinges of dimensional interaction:

Edge (ρ→Ψ hinge):
• ~10⁸–10²² Hz Overlap

• Under 10⁸ Hz ρ dominates, Ψ is faint.
• Lower anchor at 10⁸ Hz: onset of light-like transport governed by c. Quantum tunneling, qubit spreading and neural/biological overlaps occur here.
• Upper limit ~10²² Hz where wavefunctions dominate → quantum onset.

Edges (hinges):
• ρ→Ψ hinge: onset of coherence coupling (~10⁸–10²² Hz)

• Ψ dominates from 10⁸ to 10²⁵ Hz
• Ψ→Φ hinge at ~10³²–10³³ Hz: inner boundary where wavefunctions extend into coherence fields.

Higgs overlap

• Ψ→ρ Lower mass band 10²⁵–10²³ Hz: localized mass formation.

• Φ→Ψ→ρ Cascade 10³³–10²³ Hz: with Φ stabilizing those masses.

• 10²⁵–10³² is a "mixed" domain of Ψ and Φ –where most instabilities and decays occur.

Edge (Ψ→Φ hinge):
• ~10³²–10³³ Hz: inner edge → marks the transition from quantum to coherence field. Entanglement thresholds, stabilization.

Envelopes

• Speed of light (c): 10⁸–10⁴³ Hz is both velocity limit in 3D (ρ) and wave-rate in 4D (Ψ).
• Hubble rate (H ~10⁻¹⁸ s⁻¹): global envelope frequency, modulating expansion across the entire ladder.

Electromagnetism

At low frequencies, it defines classical perception (heartbeat Hz → light). 1–10¹⁴ Hz

At mid-band, it controls quantum devices (GHz → THz) starting at the ρ→Ψ overlap.

At high bands, it sets mass-energy and coherence stability (10²³ Hz → Higgs at 10²⁵ Hz).

At the extreme, it merges with gravity as the Planck scan rate (10⁴³ Hz).

DM identified a ladder of coherence access points by geometrically scaling down this frequency in powers of 10³, 10⁶, and 10¹⁰. These yield key GHz frequencies that align with coherence transitions:

15.83 GHz ⇄ 3D (ρ) to 4D (Ψ) coherence transition
18.5 GHz ⇄ Quantum peak resonance (Ψ)
31.6 GHz ⇄ 4D (Ψ) to 5D (Φ): Entanglement activation zone and breakdown frequency.
37.0 GHz ⇄ Entanglement frequency (Φ): Quantum non-locality access.

These frequencies correlate with stabilization thresholds where decoherence occurs due to environmental interactions, material noise, or quantum tunneling thresholds (with device-specific detuning). Where coherence decay along s:

Γeff = Γ₀ e^(–s / λₛ)

Fabricated Qubits (Engineered)

Qubits sit in the ρ–Ψ overlap window ~10⁸–10²² Hz. This is the domain where localized 3D systems begin to behave as distributed wavefunctions. It is the engineering-accessible region, covering GHz-scale quantum devices, BECs, and other lab-based coherence experiments. Qubits spread at ~10⁸-10¹¹ Hz, where c begins to govern coherence transport. Being constructed in 3D hardware, they do not naturally start at the same coherence frequencies as fundamental particles

Their GHz resonances sit exactly in DM’s ρ–Ψ crossover window. By refining qubit engineering around these dimensional gates, DM outlines a pathway for coherence-based technologies.

Base qubit frequency (~GHz) ⇄ anchoring in 3D resonance (ρ hardware).

10–20 GHz ⇄ coherence spread across Josephson junctions (ρ → Ψ window).

15–20 GHz region ⇄ engineered qubits converge with the natural ρ → Ψ transition zone.

30–40 GHz ⇄ access to Ψ → Φ effects in superconducting entanglement labs.

This explains why fabricated qubits appear fragile: they climb upward into alignment from the 3D side, rather than stabilizing naturally in the 4D/5D coherence domains.

Natural particles inhabit a clean geometric ladder dictated by Planck scaling. Fabricated qubits begin at lower anchors due to 3D construction, then converge toward the same coherence thresholds. Both are ultimately governed by the same DM coherence hierarchy, but their entry points differ.

Qubits should phase-lock to envelopes and be treated as dimensional travelers. By aligning with coherence gates, synchronizing to envelopes, and adopting hypercubic construction, quantum computing can move beyond fragile trial-and-error devices to robust coherence-based technologies.

Instead of relying solely on cryogenics, qubits can be phase-shielded using electromagnetic modulation aligned with c = ℓₚ/tₚ. Shielding at coherence edge frequencies would suppress unwanted tunneling.

Quantum computing today faces its greatest limitation in qubit decoherence. Conventional approaches treat decoherence as a material or noise problem. The Dimensional Memorandum reframes decoherence as a dimensional coupling issue.

Recent astrophysical discoveries map cleanly onto this ladder:

Tidal disruption events (TDEs) detected in dusty galaxies by JWST occupy the ρ band (~10¹³–10¹⁶ Hz), where Ψ→ρ boundary crossings dominate.

Awakening AGN and young radio galaxies (~10¹⁸–10¹⁹ Hz) fall within the lower Ψ band, reflecting recursive oscillations and fresh jet alignment.

Mass-gap mergers (GW231123) at ~10²⁴ Hz occur within the Ψ regime, interpreted as coherence braids merging across s-depths.

Primordial black holes (~10⁴⁰ Hz), direct-collapse SMBHs (~10³⁸ Hz), extreme-mass black holes (≥10¹⁰ M☉, ~10³⁹ Hz), and dense SMBH clusters (~10³⁸ Hz) are Φ-dominated states, coherence hubs forming directly at higher s-depths.

This mapping demonstrates that black holes, often treated as disparate anomalies in standard astrophysics, instead represent ordered coherence states along a single geometric spectrum (ρ → Ψ → Φ).

DM predicts measurable signatures for each band, including polarization stability, suppressed high-frequency flicker, gravitational-wave coherence shoulders, and phase-coherent lensing arcs.

Magnetar electromagnetic effects:

• Vacuum birefringence: Optical to X-ray bands (10¹⁴–10¹⁸ Hz).
• Photon splitting: Gamma-ray regime (10²⁰–10²² Hz).
• Persistent hard X-rays: (10¹⁸–10²¹ Hz).

Magnetars provide natural laboratories for testing DM predictions.

Mass and Lifetime

The DM Mass Formula

The DM mass formula is given by:

mₙ = Eₚ · e^(–n / λₛ)

where:
mₙ = particle mass-energy.
Eₚ = Planck energy = √(ħc⁵ / G) ≈ 1.22 × 10¹⁹ GeV.
n = coherence step number.
λₛ = coherence scaling constant, typically of order unity.

This formula reflects how mass arises from successive projections of 5D coherence (Φ) into 4D wave states (Ψ) and finally into localized 3D matter (ρ).

Coherence field gives rise to wavefunctions (Φ → Ψ).

Wavefunctions collapse to mass (Ψ → ρ).

Coherence Depth (s)

To pinpoint any particle: measure mass (m), compute s depth using equation below, determine the lifetime ratio /tₚ, and use DMs ladders.

The coherence depth (s) for a particle is defined as:

s = √[-ln(m / m_max)]
where m_max = 173,100 MeV (Top Quark mass).

A smaller s indicates a particle is more localized in 3D (ρ), while a larger s means it is more wave-like and less massive, residing deeper in the 5D coherence field (Φ). For massless particles like photons, s → ∞.

Family Scaling Steps

The energy hierarchy between particle families (leptons, quarks, and bosons) follows geometric scaling steps, often close to powers of 10⁶, which reflect the transition between nested tesseract layers. This leads to an extended formula:

mₙ,ₖ = Eₚ · 10⁽⁻⁶ᵏ⁾ · e^(–n / λₛ)

where k is the family index.

By scaling particle properties relative to Planck units, we reveal a clear geometric relationship between mass, quantum coherence, and stability.

Particle masses and lifetimes can also be scaled relative to Planck energy (Eₚ ≈ 1.22 × 10¹⁹ GeV) and Planck time (tₚ ≈ 5.39 × 10⁻⁴⁴ s). These ratios reveal how far each particle is from the Planck scale:

Mass ratio: m / Eₚ.
Lifetime ratio: τ / tₚ.

Stable particles have lifetime ratios >10⁴⁴, while short-lived particles have ratios much smaller, correlating with low coherence.

Each particle’s mass relative to Planck energy (m/Eₚ) reveals its geometric step along the ρ → Ψ → Φ ladder.

Top quark and Higgs are close to the highest energy step, while electrons and photons lie many orders of magnitude lower, aligning with the 10⁴³ frame-rate ratio.

The powers of ten (10³, 10⁶, 10¹⁰, etc.) observed between particles match the scaling intervals seen between Planck units and cosmic scales (10⁶¹ in distance, 10⁶⁰ in time).

Particle Coherence Mapping

Mass (MeV/c²) → Measured rest mass

s (Coherence Depth) → DM coherence position (ln-based)

m / Eₚ → Mass fraction relative to Planck mass

10^x (mass) → Log10-scaled mass representation

Lifetime (s) → Experimental lifetime (if applicable)

τ / tₚ → Lifetime to Planck time ratio

Energy (eV) → Converted from MeV

Frequency (Hz) → E / h calculation

f / fₚ → Frequency as fraction of Planck frequency

s-depth (ln-scale) → Derived from ln(m/m_max)

Planck mass ≈ 1.22 x 10²² MeV

Planck time ≈ 5.39 x 10⁻⁴⁴ s

Planck frequency ≈ 1.85 x 10⁴³

Decay

Coherence Ancestry Equation

ΔIₙ = ∑ (ΔTⱼₖ + ΔT̄ⱼₖ) · e^(–s / λₛ)

Here Iₙ is the detected channel’s coherence, ΔTⱼₖ the transition amplitude from ancestor order j along branch k, and λₛ the coherence decay length. Ancestors j = {3,4,5} correspond to ρ, Ψ, Φ dimensional orders; k denotes fermion, boson, or Φ-node branches.

Muon → Electron + ν_μ + ν̄_e

Muon decay reflects time-compressed identity unraveling:

Φ_μ → Φ_e + Φ_ν_μ + Φ_ν̄_e

• Muon = time-dense electron phase field
• Coherence unraveling redistributes identity into 4D projection
• Neutrinos = coherence flow paths

Higgs → ZZ / WW / Fermion pairs

Higgs field is a 5D coherence stabilizer node:

Φ_H → Φ_Z + Φ_Z or Φ_W + Φ_W or Φ_fermion + Φ_fermion

• Higgs decay reveals pathways of coherence mass generation
• Each decay reflects dimensional rebinding of identity across s

Neutron → Proton + Electron + Antineutrino

Standard beta decay becomes a coherence cascade:

Φ_n → Φ_p + Φ_e + Φ_ν̄

• Neutron = deeply stabilized recursive coherence state
• Decay triggered by decoherence in s
• Antineutrino = unbound coherence residue

Kaon → Pion + Photon

Meson collapse under wave-function gradient stress:

Φ_K → Φ_π + γ

• Photon carries phase energy of coherence decay
• Kaon and pion differ by resonance structure in s
• Collapse governed by symmetry instability in T̄_i

Antiparticles

ΔIₙ = Σ (ΔTⱼₖ + ΔT̄ⱼₖ) · e^(−s / λₛ)

• ΔTⱼₖ = forward coherence transition (particle channel).
• ΔT̄ⱼₖ = mirrored/inverted transition (antiparticle channel).
• j = {3,4,5} anchors the dimensional layer (ρ, Ψ, Φ).
• k = fermion, boson, or Φ-node path.

Antiparticles are the natural conjugates (ΔT̄) of particle coherence cascades.

Conjugate Coherence Residues

• Beta decay:
Neutron → Proton + Electron + Antineutrino
Φₙ → Φₚ + Φₑ + Φ_ν̄
→ The antineutrino is the ΔT̄ branch residue, carrying away inverted coherence.

• Muon decay:
Muon → Electron + ν_μ + ν̄ₑ
Φ_μ → Φₑ + Φ_νμ + Φ_ν̄e
→ The anti-electron neutrino is the conjugate channel required to balance the time-compressed identity release.

• Kaon decay:
Kaon → Pion + Photon
Φ_K → Φ_π + γ
→ Neutral kaons (K⁰) mix into K⁰ and anti-K⁰ pairs. This is the Ψ–Φ interference of ΔT and ΔT̄ channels.

• Higgs decay:
Higgs → ZZ, WW, fermion–antifermion
Φ_H → Φ_f + Φ_f̄
→ Fermion/antifermion pairs emerge by necessity — the Higgs is a Φ stabilizer node, and releasing coherence requires mirrored identity outputs.

Geometric Interpretation

• In 3D (ρ): antiparticles appear as mirror matter with opposite charge/quantum numbers.
• In 4D (Ψ): they are the conjugate half of the same wavefunction.
• In 5D (Φ): both are unified as one symmetric coherence object, split only by projection.

Thus, antiparticles are not separate entities but the mathematical requirement of coherence inversion across s-depth.

Decay mappings in DM inherently include antiparticles: they are the ΔT̄ branches. Antiparticles exist because geometry forces every ΔT to be paired with a ΔT̄, ensuring coherence conservation in Φ even when ρ projections appear asymmetric.

Antiparticles are Ψ-level mirrors created by time reversal symmetry, but their abundance and stability are set by Φ topology. In DM, particles and antiparticles are not simply opposites; they are linked across dimensional projections, with the Φ domain acting as the asymmetry engine.

This projection explains certain observed features of reality:
• Inverted coherence states: Seen in oscillations, dual resonance modes, and mirrored quantum behavior.
• Cosmic filaments: Large-scale structures in the universe reflect projected coherence filaments from the 5D lattice, appearing as mirrored or doubled structures in 3D.

This mirrors the role of the Dirac equation, where negative- frequency solutions naturally correspond to antiparticles.

Dirac equation with positive and negative frequency solutions:

(iγ^μ ∂_μ - m) ψ(x,t) = 0

Antiparticle as a phase-conjugate mirror:

ψ_antiparticle ~ Ψ*(x, -t)

Particle vs antiparticle amplitudes in DM:

A_+(s) = ∫ e^(−s/λₛ) W_+(s) ds

A_−(s) = ∫ e^(−s/λₛ) W_−(s) ds

Net asymmetry:

Δ = (A_+ − A_−) / (A_+ + A_−)

Antiparticles in DM are not mysterious opposites but required conjugates of coherence transitions. They emerge naturally from ΔT̄ channels, align with Dirac negative-frequency solutions, and explain both particle decays and cosmic asymmetry. DM shows that particles and antiparticles are unified in Φ, divided only by projection into Ψ and ρ.

Forces

Gravity: Global curvature stabilizer

Emergent from full Φ(x, y, z, t, s) coherence (5D)

s-depth: s ≈ 0.00

Electromagnetic (EM)

Wave stabilization and entanglement field

Propagates via Ψ(x, y, z, t) coherence (4D)

s-depth: s ≈ 0.8–4.0

Weak

Particle type transformation field

Appears during coherence destabilization (4D–3D boundary)

s-depth: s ≈ 2.5–3.5

Strong

Local particle glue

Confines ρ(x, y, z) in decoherent low-s states 3D

s-depth: s ≈ 3.5–4.0

Gravity is global (Φ) but weak in local particle physics. Strong and weak forces are local (ρ/Ψ) and confined to nuclei. Only EM bridges the entire ladder.

Electromagnetism (EM) occupies a unique and pivotal role. Unlike the other fundamental forces, EM spans across all dimensional domains—localized 3D (ρ), wave-based 4D (Ψ), and coherence-stabilized 5D (Φ). This makes EM the universal hinge that allows transitions between domains.

Electromagnetism is not just one force among four. It is the lever—the single field humanity can control in the lab that directly interfaces with higher-dimensional coherence.

Gravity, Dark Energy and Dark Matter — the Λ-Gap

These anomalies trace back to the same geometric depth factor — the Λ-gap of ~10¹²².

In conventional physics, Gravity appears ~10³⁶ times weaker than electromagnetism at the particle scale. This hierarchy problem has resisted explanation. In DM, gravity’s apparent weakness arises naturally from its projection across the s-depth of the 5D coherence field.

Gravity originates in the Φ-field, G_μν = κ ⟨∂ₛ Φ_μν⟩. To manifest in 3D, it must project across the Λ-gap of ~10¹²² Planck steps. This projection dilutes its apparent strength, producing the observed weakness.

• Φ → ρ projection compresses matter.

Dark energy is the residual envelope of this projection, the observable fraction of Φ stabilization at cosmological scales. The Λ-gap (~10¹²²) bridges Planck frequency (10⁴³ Hz) with the Hubble rate (~10⁻¹⁸ s⁻¹). This explains the small but nonzero value of Λ observed in cosmology.

• Φ → Ψ → ρ projection expands space via the Λ-envelope.

Dark matter arises as a stabilization effect of the Φ field within the Ψ (wave) domain. It corresponds to coherence fields projected across the Λ-gap (~10¹²² Planck steps). Because this depth ensures decoherence at the particle scale, dark matter cannot be directly detected as localized ρ states, but only via its global effects (rotation curves, lensing maps, and cosmic structure).

• Φ → Ψ stabilization without direct ρ collapse.

Dark matter represents Φ anchoring into Ψ bands:
Φ(x, y, z, t, s) → Ψ(x, y, z, t) = ∫ Φ(x, y, z, t, s) · e^(–s / λₛ) ds
This stabilizing effect produces gravitational halos and large-scale coherence scaffolding for galaxies.

Gravity weakening:
F_gravity / F_EM ∼ e^(−s / λₛ), with s ≈ 10¹²²

Dark energy suppression:
Λ_eff = Λ_s · e^(−s / λₛ)

Each depend on the same exponential suppression factor across ~10¹²² steps.

Λ-gap of ~10¹²²: This factor represents the depth of coherence projection from Planck-scale processes into the observable universe. DM shows that the apparent mysteries are natural consequences of geometry.

Geometry

The Code of Reality

This section describes how each Planck equation aligns with DM's dimensional hierarchy and why these constants arise from the structure of space and time itself.

These constants define the resolution (lₚ), frame rate (tₚ), and energy thresholds (Eₚ) of reality's nested dimensional structure:

Planck Length (lₚ)

The Planck length is given by:
lₚ = √(ħG / c³) ≈ 1.616 × 10⁻³⁵ m

In DM, lₚ defines the smallest measurable unit of 3D space. 3D (ρ) reality is structured as a mosaic of Planck-length units. This aligns with localized, classical states that emerge from the projection of higher dimensions. The Planck length thus represents the geometric resolution of 3D (x, y, z) reality.

Planck Mass (mₚ)

Represents the mass contained in a Planck volume at energy Eₚ.

mₚ ≈ 2.176 × 10⁻⁸ kg is the mass at which gravitational effects become inseparable from quantum behavior.

In DM, Eₚ defines the energy state required for ρ → Ψ → Φ transitions. Mass is a geometric property rather than an intrinsic constant. The effective mass depends on the coherence depth along the fifth-dimensional axis (s), described by:

m_effective = m₀ e^(–s / λₛ)

where λₛ is the coherence length scale.

This formulation explains the relativistic effects on mass and the apparent variation of mass in extreme energy conditions, such as near the speed of light or within strong gravitational fields.

Planck Time (tₚ)

Planck time is defined as:
tₚ = √(ħG / c⁵) ≈ 5.39 × 10⁻⁴⁴ s

In DM, tₚ is the 'frame rate' of reality. Time is not an independent dimension but the progression of a cube through a tesseract. Each tick of Planck time corresponds to one frame (scan rate), resulting in approximately 1/tₚ ≈ 1.85 × 10⁴³ frames per second. The speed of light (c) naturally arises from this relationship — as c = lₚ / tₚ, which DM describes as the universal scanning speed of 4D (x, y, z, t) geometry.

Planck Energy (Eₚ)

Planck energy is defined as:
Eₚ = √(ħc⁵ / G) ≈ 1.22 × 10¹⁹ GeV

In DM, Eₚ represents the threshold for transitioning from 4D quantum states (Ψ) to 5D coherence fields (Φ). At or above this energy → matter exhibits coherence phenomena such as those observed in the early universe, black holes, or in high-energy collisions. Planck energy thus marks the boundary between conventional quantum mechanics and the deeper coherence-driven structure of Φ(x, y, z, t, s).

Local

Wave

Coherence

Planck-to-Cosmos ratio (~10⁶¹)

Planck length (lₚ ≈ 1.616 × 10⁻³⁵ m) defines the smallest quantum unit of space, while the observable universe has a radius of approximately R_obs ≈ 4.4 × 10²⁶ m. The ratio between these scales is:

R_obs / lₚ ≈ 4.4 × 10²⁶ m / 1.616

10⁻³⁵ m ≈ 2.7 × 10⁶¹

A similar ratio appears in time:

T_age / tₚ ≈ 4.35 × 10¹⁷ s / 5.39

10⁻⁴⁴ s ≈ 8 × 10⁶⁰

The Planck-to-Cosmos ratio (~10⁶¹) connects the smallest quantum scale (lₚ) with the largest cosmic scale (R_obs). This ratio is not coincidental but emerges from the geometric progression of dimensions.

The fact that both the distance and time ratios (~10⁶¹ and ~10⁶⁰) match observational data, is evidence that this cosmic-to-quantum mirror symmetry is a fundamental feature of reality.

Planck's power of ten scaling naturally corresponds to the 10 tesseracts, that form the boundary of a 5D penteract. Each tesseract can be viewed as a 10⁶ order-to-the-magnitude scaling step — spanning from the smallest Planck cell to the largest cosmic region.

These ratios indicate that they're contained in the same (measurable) geometry, scaling together (endpoints of the same sequence). The combined ratios (~10¹²¹ total plank cells) is effectively the volume of the 4D tesseract and the full Universe is ~10¹²² total Planck cells.

Higgs Field

~125 GeV (1.25 × 10⁻²⁵ kg).

Cosmic scale (10²⁶ m)

⇅ 10⁴³

Higgs scale (10⁻¹⁸ m)

⇅ 10²⁶

Planck scale (10⁻³⁵ m)

The Planck time tₚ ≈ 5.39 × 10⁻⁴⁴ s, meaning reality 'ticks' at:
fₚ = 1 / tₚ ≈ 1.85 × 10⁴³ Hz.

The energy ratio between the Planck energy (Eₚ ≈ 1.22 × 10¹⁹ GeV) and the cosmic critical energy density is also approximately 10⁴³. This ratio links the Higgs energy scale to cosmic expansion, suggesting that local mass generation and universal evolution are synchronized.

The Planck length is lₚ ≈ 1.616 × 10⁻³⁵ m, while the observable universe has a radius of approximately R ≈ 4.4 × 10²⁶ m. Their ratio is:
R / lₚ ≈ 10⁶¹.

Similarly, the total mass-energy content of the universe compared to the Planck mass (~2.18 × 10⁻⁸ kg) aligns with this 10⁶¹ scaling. This ratio defines the spatial and mass hierarchy from quantum to cosmic structures.

(Magnitude anchor)

Ψ (4D coherence amplitude)

ρ (3D localization scale)

Vacuum fluctuations and amplitude

Mass is defined by how strongly particles couple to this scalar field

Vacuum expectation value

Nonzero in empty space

Localized matter

Quantum waves

When collapsing from Ψ (4D waves) into ρ (3D particles) “direction” is lost; only the magnitude scaling remains, encoded in these powers of ten hierarchies

The core exponential law governing all mass, frequency, and coherence relationships is:

m = Eₚ e^{-s / λₛ}

where:
m = observed rest mass (or equivalent energy)
Eₚ = √(ħ c⁵ / G) ≈ 1.22×10¹⁹ GeV = Planck energy
s = coherence depth (dimensionless projection depth from 5D → 4D)
λₛ = coherence scaling constant (≈ 1 for particle domain; ≈ 10¹²² between Planck and cosmic scales)

Compact Equation Set

m(s) = E_P e^{−s / λₛ}
f(s) = f_P e^{−s / λₛ}
Λ_eff(S) = Λ_P e^{−S / λₛ}
σ(m) ∝ e^{−m / λₛ}

Frequency Form

Using E = h f, the frequency version of the exponential law becomes:
f = fₚ e^{−s / λₛ}, where fₚ = 1 / tₚ ≈ 1.85×10⁴³ Hz.

Example:

Electron: 1.24×10²⁰ Hz ≈ 3.77 s-depth

Muon: 2.56×10²² Hz ≈ 2.38 s-depth

Proton: 2.27×10²³ Hz ≈ 1.99 s-depth

Top quark: 3.0×10²⁵ Hz ≈ 0.05 s-depth

A semilog plot of log(m/Eₚ) vs s shows a perfect line:
Top Quark (0.05) — Higgs (0.57) — W/Z (0.8) — Proton (2.0) — Muon (2.4) — Electron (3.8)
All align along the same exponential curve — the DM coherence law.

Coherence Ladders

(10³ → 10⁶ → 10¹⁰) Captures local and subatomic transitions.

(10⁶¹ → 10¹²¹ → 10¹²²) Captures the dimensional structure of the cosmos, from the 3D observable span to the 4D tesseract volume, and the 5D penteract coherence field.

Together, these ladders form a complete geometric map of reality, connecting microphysics and macrophysics, that tie directly to the Planck-to-Cosmos ratio

These mirrored ratios imply that the universe's expansion, particle masses, and quantum coherence are all governed by a single set of geometric principles. For example:

• The Higgs field connects 10⁴³ energy scaling with mass generation.
• Dark energy reflects 10⁴³ coherence expansion across 10⁶¹ spatial scales.
• Black hole entropy and information bounds match these ratios.

Planck units naturally are dimensional projections. The alignment shows that geometry itself is the foundation of all physical laws.

The DM’s nested dimensional structure matches exactly to the Coxeter group symmetry sequence B₃ → B₄ → B₅. The scaling ratios of DM’s Planck cell counts (~10⁶¹, ~10¹²¹, ~10¹²²) align precisely with the volumetric scaling rules of higher-dimensional Coxeter lattices, providing a direct geometric explanation for particle mass distributions, coherence bands, and cosmic structure.

Axis Orthogonality Statement

Mathematical Formulation:

𝒢 = ℤ(10⁴³) ⊕ ℤ(few × 10⁶¹)

This expresses that all placements of physical scales exist as lattice points in the discrete group 𝒢, where the two orthogonal axis correspond to fundamental scaling constants: one at the Planck frequency scale (~10⁴³ Hz) and another at the large-scale cosmic boundary (~10⁶¹ in length scaling). The direct sum ⊕ enforces orthogonality between these axis, meaning changes in one do not alter coordinates along the other.

Coxeter Volumetric Growth Constraint

Mathematical Formulation:

V(Bₙ₊₁) / V(Bₙ) ∝ 10ᵏⁿ ⇒ (k₃, k₄, k₅) ≈ (3, 6, 10)

This constraint comes from the volumetric scaling ratios of Coxeter polytopes (or dimensional boundary volumes). The ratio of the volume of a boundary object in dimension n+1 to that in dimension n follows an exponential scaling law determined by kₙ. The approximate values (3, 6, 10) correspond to 3D → 4D → 5D growth steps. These scaling exponents are consistent with DM's predictions for dimensional nesting and the hyper-volume growth of geometric boundaries.

kₙ = C(n,2) = n(n–1)/2

This formula counts the number of independent 2D planes you can form from n orthogonal axes.

The numbers 3, 6, and 10 are simply the geometric footprint of dimensional growth. They are encoded in the Coxeter group Bₙ, which governs hypercubic symmetry. In DM, these numbers directly control scaling ladders (10³, 10⁶, 10¹⁰ in microphysics) and their cosmic mirrors (10⁶¹, 10¹²¹, 10¹²²).

Dimensional Nesting

Simple Boundary Logic

Φ 5D Boundary: Field

Penteract faces → Tesseracts

Hyper-volumetric surfaces with shared spatial points, all space and time are merged as coherence.

Stabilized Coherence

Φ(x, y, z, t, s)

Geometric anchors: gravity, Big Bang, black hole cores, dark energy, dark matter, entanglement, Higgs field

Ψ 4D Boundary: Wave

Tesseract faces → Cubes

Volumetric surfaces spanning time

Partial Coherence, not stabilized in s

Ψ(x, y, z, t)

Wavefunctions: time merged coherence, particles spread, superposition, time dilation

ρ 3D Boundary: Local

Cube face → Planes

Perceives cross-sections of time and space

Incoherent to t and s

ρ(x, y, z)

Localized: fixed position, discreet measurable objects, localized particles

Decoherence

➝

Field of Space/Time

1 (Φ) = full coherence

➝

Wave of Time

1/10 (Ψ) = one dimension “hidden” → time becomes a wave

➝

Localized

1/8 of 1/10 (ρ) = two levels down → matter appears localized (but as cross-sections)

Boundary Logic:

Each dimension (3D, 4D and 5D) follow the same geometrical nested hierarchy. Any objects within their respective dimension, moves strictly based on their axis of movements, x, y, z, t and/or s. This decides physical laws per dimension. (All dimensions follow this hierarchy.)

(Φ) 5D: moves within boundaries of length, width, height, time, space perceiving in 4D hyper-volumes.

(Ψ) 4D: moves within boundaries of length, width, height, time perceiving in 3D volumes.

(ρ) 3D: moves within boundaries of length, width, height perceiving in 2D planes.

(⟂) 2D: a 3D observer's cross-sections of t and s.

"Length" no longer applies in the classical sense. What remains is a stilled wave. (mass=E/c²=hf/c²) Mass equals frequency-based energy. The Planck Length (Lp ≈ 1.616 × 10⁻³⁵ m) marks the cutoff scale where coherence between space and time collapse. Below this, "length" does not behave as an extension—it becomes the boundary surface of space and time. (Explaining why quantum behavior dominates and classical physics fails.)

3D Observer Perspective: (⟂)

Cube faces → Squares (planes)

Planar surface areas (faces) are the geometric consequence of 3D and the flow of information.

When you look at a cube or sphere, you perceive its faces (⟂) — never the full interior/exterior structure at once.

Sensory Examples

Touch = Specifically reliant on contact with planar boundaries (⟂).

1–1000 Hz

Hearing = Pressure waves interact with eardrum (⟂) across surfaces (⟂) of air density waves.

20–20k Hz

Visual = Eyes collect 2D projections of 3D surfaces (⟂). Light bounces off surfaces (⟂) into our retinas (⟂) and we infer depth — still surface-limited in direct visual input. Look at a photo, it doesn't have depth, but you infer.

4×10¹⁴ – 7×10¹⁴ Hz

The CMB data implies a flat universe (⟂), which exhibits our ability to define space, time, or mass from a 3D perspective.

Geometric Time

3D observer: The cross-section of 4D, experienced in 2D frames (faces) ⟂

(Ψ→ ρ → ⟂ = t)

In special relativity, E = mc² emerges from Lorentz invariance and the constancy of c. Quantum theory, meanwhile, treats the wavefunction in an abstract Hilbert space. The DM framework embeds both within a nested geometric hierarchy:

ρ (3D localized), Ψ (4D wave), and Φ (5D coherence). Here, c is the scan speed that advances 3D faces through 4D frames, hence it plays a dual role as both causal speed limit and geometric necessity.

c = ℓₚ / tₚ
Simultaneously, the frame rate of this scan is the Planck frequency:

fₚ = 1 / tₚ
A 3D localized mass (m) is a ‘stilled wave’—energy constrained to ρ. Releasing that localization exposes the underlying 4D wave energy, and the conversion is governed by the scan rate c. Thus, the energy content associated with mass (m) is:

E = m c²

Interpreting mass as a localized wave explains why E = mc² holds universally—energy and mass are two presentations of the same entity.

Time is a 3D cube revolving through a 4D tesseract, consecutively perceiving cube faces (⟂):

Rate ≈ 1 / tₚ ≈ 1.85 × 10⁴³ faces per second

This 'face rate' (⟂) is the frame rate of 3D reality. Each Planck tick corresponds to one face transition of the 4D tesseract, progressing the 3D universe forward in time — each scale jump also crosses the penteract. (Eames' Powers of Ten concept mirrors how 4D scanning operates)

Dimensional Memorandum reframes physics as a fully geometric system where perception, particles, forces, and time itself emerge from structured coherence transitions between dimensions.

The 3D world is a cross-section of a vast 5D coherence lattice—a flickering sequence of stabilized information frames projected into our awareness at Planck resolution. Everything we observe is merely a face of a deeper structure.

In 3D, faces are 2D surfaces → particles appear on flat detectors. In 4D, faces are 3D volumes → wavefunctions spread volumetrically. In 5D, faces are 4D hypervolumes → entangled states sharing space and time in full coherence.

DM clarifies- that reality is not built from particles or waves alone, but from coherence—the underlying field binding existence across all of space and time (entanglement is localized coherence). Once this is understood, unifying quantum mechanics, gravity, consciousness, and cosmology becomes not only possible—but inevitable.

Subjective Mass

~10¹²²

S = ∇ₛ² Φ - Λₛ e^(-s/λₛ)

Objective Identity

"Length" no longer applies in the classical sense?

(ρ) (Ψ) (Φ)

Dimensional Memorandum

T' = T · √(1 – v²/c²)

x, y, z, t, s

Activation Threshold

~10³³-10⁴³ Hz

astrophysical phenomena

Orientation

(c = lₚ / tₚ)

s-depth: s ≈ 0.8–4.0

Originated 2023, Presented 2025

Author: J. Theders

biological quantum systems

Mass = Localized wave without time (t)

10²⁵ Hz

10³³-10⁴³

10⁴³

mₙ = Eₚ · e^(–n / λₛ)

Γeff = Γ₀ e^(–s / λₛ)

energy thresholds (Eₚ)

Physical Laws

Geometry 101

10¹⁵ Hz

Particles below this threshold

𝓘ₙ = ∑(Tᵢ + T̄ᵢ) · e^(–s / λₛ)

Where is Space?

When is Time?

𝓛DM = (c⁴ / 16πG)(R + S) + 𝓛ρ + 𝓛Ψ + 𝓛Φ

Dimensional Memorandum: Across Physics

This presents a consolidated validation of the Dimensional Memorandum (DM) framework against recent experimental and theoretical results across particle physics, quantum mechanics, gravitation, and cosmology. The objective was to identify contradictions; none were found. Instead, DM consistently provides the geometric skeleton underlying observed phenomena. QCD-calculated hadron masses align with DM’s coherence depth clustering, quantum experiments reveal recursive coherence consistent with DM’s Φ-field projections, cosmological surveys match DM’s Planck-to-cosmos scaling, and fundamental constants emerge naturally from dimensional nesting. These findings elevate DM to a unifying geometric framework for physics.

Introduction

Physics currently operates under these theories: Quantum Mechanics (QM), Quantum Chromodynamics (QCD), the Standard Model (SM), and General Relativity (GR). Each is precise in its domain but lacks integration. The Dimensional Memorandum (DM) framework introduces dimensional nesting — ρ (localized), Ψ (wave), and Φ (coherence) layers — with coherence depth (s) as the unifying axis. This section reviews confirmations of DM across domains.

1. Particle Physics: QCD Alignment

Lattice QCD provides numerical hadron masses, but not their geometric organization. DM predicts exponential suppression relative to the Planck scale, clustering particles in s-depth bands. Data analysis shows:

• Proton (938 MeV), Neutron (939 MeV), Pion (135 MeV), and Kaon (494 MeV) fall in the Ψ coherence band.
• Quarks stratify in ordered s-depth layers: light quarks (u, d, s) at higher s, heavy quarks (c, b, t) at low s.
• Bosons (W, Z, Higgs) sit near s ≈ 0.5–1.0, the Higgs stabilization threshold.

2. Quantum Experiments

Recent advances in quantum science provide repeated confirmation of DM principles:
• Caltech (2025): Hyper-entanglement across internal and motional states, matching recursive identity stabilization.
• Oxford: Distributed quantum computing and entangled optical clocks, validating coherence-stabilized time evolution.
• Technion: Total angular momentum entanglement, confirming recursive (Tᵢ + T̄ᵢ) binding.
• Hiroshima: Photon delocalization, demonstrating Φ-field projections.
• Bell violations without entanglement (2025): Directly consistent with DM’s phase-locked coherence channels.

3. Cosmology and Gravitation

Cosmological and gravitational data reinforce DM’s framework:
• Euclid survey: Cosmic web geometry matches Φ-skeleton projections.
• DESI: Dark energy decay consistent with Λ_eff = Λ_s e^(−s/λ_s).
• JWST: Early galaxy clustering aligns with DM’s dimensional nesting.
• Gravitational waves (O4a, GW231123): Remnants cluster in coherence bands, with ringdown signatures predicted by DM.
These findings place DM as a coherence geometry unifying GR and cosmology.

4. Fundamental Constants

Fundamental constants — Planck units, fine-structure constant, proton–electron mass ratio, Rydberg constant, flux quantum, Josephson constant — emerge from DM’s projection rules (ρ → Ψ → Φ). For example:

• Planck length and Planck time define the scanning resolution of 4D wavefaces.
• The fine-structure constant α arises from dimensional ratio constraints.
• Proton–electron mass ratio μ reflects nested s-depth scaling.
• The Josephson and von Klitzing constants are direct coherence quantization rules.
DM demonstrates these constants are not arbitrary but geometric.

5. Synthesis Across Domains

No mismatches were found between DM predictions and data. Instead:
• QCD: Hadrons fall into coherence clusters.
• QM: Entanglement anomalies confirm coherence-first interpretation.
• GR & Cosmology: Structure formation and dark energy decay match DM scaling.
• Constants: Derived from projection rules.
Together, these results show DM as the unifying geometry across physics.

Conclusion

The Dimensional Memorandum framework was stress-tested against data across particle physics, quantum mechanics, gravitation, and cosmology. No contradictions were found. Instead, repeated confirmations emerged, with DM providing geometric explanation where conventional theories provide numerical fits. DM thus offers a predictive, testable, and unifying model of physical reality.

Particle Frequencies

For each particle, the Compton frequency is calculated using the relation:
f_compton [Hz] = (mc²) / h = 2.41799 × 10^14 × m [eV]

This table summarizes Standard Model particle masses and their corresponding frequencies, aligning them with the Dimensional Memorandum (DM) frequency bands (ρ, Ψ, Φ). Neutrino values are shown as ranges due to mass uncertainty; quark masses are scheme-dependent.

Notes:
• Frequencies derived from Compton relation using CODATA constants.

• Neutrino frequencies shown as bands (< 1 eV).

• Quark masses are scheme-dependent (e.g., MS-bar at reference scales).

• Φ (10^33–10^43 Hz) contains no SM rest-mass placements—reserved for coherence fields.

m = m₀ · e^(−s / λₛ) (Mass suppression)
t₁ = t · e^(−γₛ) (Time dilation by coherence)
Λ_eff = Λₛ · e^(−s / λₛ) (Vacuum energy suppression)
Ψ_obs = ∫ Ψ · δ(t − t_obs) dt (Collapse projection)
G_μν + S_μν = (8πG/c⁴)(T_μν + Λₛ g_μν e^(−s / λₛ)) + ∂/∂s ∫ Φ ds (Unified field)

Experiments or observations examples include:

• Neutrino oscillation splittings (Super-K, DUNE, JUNO).
• CODATA constants: α, μ, R∞, Josephson, von Klitzing.
• LHC anomalies in particle decays.
• Black hole imaging (EHT, Sagittarius A*).
• Gravitational wave data (LIGO/Virgo/KAGRA).
• Quantum computing coherence jumps at GHz–THz frequencies.
• Quantum biology signatures in mitochondria and photosynthesis.

...

DM explains 100+ years of paradoxes with clean geometric nesting—cube → tesseract → penteract:

What?

What can be measured? (x, y, z)

ρ 3D = (x, y, z)

When?

Change introduces time. (t)

Ψ 4D = (x, y, z, t)

Where?

Where is the structure? (s)

Φ 5D = (x, y, z, t, s)

How?

Axis of Movements

(x) Length, (y) Width, (z) Height, (t) Time, (s) Space

Why?

Geometric First Principles

point, line, square, cube, tesseract, penteract

5 -D

(⟂)

Cross-section

↑

(Φ)x, y, z, t, s

Field

(Ψ)x, y ,z, t

Wave

(ρ)x, y, z

Local

↑

Dimensional Coherence and Symmetry Groups

Coxeter groups describe reflection symmetries that generate regular polytopes in any dimension.

• B₃ generates the cube and octahedron (3D).

• B₄ generates the tesseract (4D).

• B₅ generates the penteract (5D).

Each increase in dimensionality introduces a new orthogonal reflection axis — in DM, this corresponds to a new coherence coordinate that couples otherwise independent oscillations.

Thus, the progression B₃ → B₄ → B₅ mirrors the DM projection chain ρ(3D) → Ψ(4D) → Φ(5D): local matter → quantum wave → coherence field.

Wavefunction, Information, and Self

Modern interpretations of quantum mechanics often describe the wavefunction as 'mere information'—a probabilistic catalog of possible measurement outcomes. In contrast, the Dimensional Memorandum framework insists that the wavefunction is not abstract bookkeeping but a real coherence distribution, anchored in the geometry of higher dimensions. Just as human beings are not separate from the information they carry—genetic, neural, and experiential—the wavefunction itself is stabilized information expressed through geometry.

1. DM Projection Structure

The DM framework maps physical existence across three nested layers of geometry:
ρ (3D, localized) → observed matter, mass, and position.
Ψ (4D, wave) → quantum coherence, wavefunctions, entanglement.
Φ (5D, coherence) → global stabilization field, coherence anchoring, dark energy/dark matter fields.

The mappings are defined by projection equations:
Ψ(x,y,z,t) = ∫ Φ(x,y,z,t,s) · e^(−s/λₛ) ds
ρ(x,y,z; t₀) = ∫ Ψ(x,y,z,t) · δ(t−t₀) dt

Here λₛ represents coherence depth, and δ(t−t₀) defines the instantaneous 3D observational slice. Thus, the wavefunction Ψ is not just information—it is a 4D structure stabilized by Φ.

2. Human Identity as Coherence

From the DM perspective, human beings are structured information fields:
• DNA encodes biological blueprints—an information lattice in ρ.
• Neural firing patterns represent Ψ-level coherence distributions.
• Consciousness emerges as Φ-level stabilization of identity across time.

Thus, humans are not separate from the information they generate. Just as the wavefunction is real coherence, the 'self' is coherence stabilized across ρ, Ψ, and Φ. This reframes both quantum mechanics and consciousness as parallel manifestations of nested geometry.

4. Geometric Equations

1) Wavefunction projection:
Ψ(x,y,z,t) = ∫ Φ(x,y,z,t,s) · e^(−s/λₛ) ds

2) Observed state:
ρ_obs(x,y,z; t₀) = ∫ Ψ(x,y,z,t) · δ(t−t₀) dt

3) Born’s rule (as projection measure):
p_i = |⟨e_i|Ψ⟩|² = overlap measure of Ψ with ρ-subspace.

4) Identity stabilization:
I = ∫ Ψ_neural(x,t) · e^(−s/λₛ) ds

In this framing, both particles and human beings are coherence-stabilized information structures.

Neural Frequencies and Coxeter Symmetry

5. Neural Oscillations as the B₃ Base Symmetry

Human neural activity occurs in the 1–10³ Hz range, which is many orders of magnitude below electromagnetic propagation limits. At these frequencies, the spatial and temporal symmetries of biological tissue are strictly 3-dimensional — they obey B₃ (orthogonal cubic) reflection symmetry. Every action potential or cortical oscillation is a localized ρ-domain event, constrained to 3D Euclidean geometry.

This places neural firing firmly within the B₃ subgroup of the larger hypercubic system.

6. The 10⁸ Hz Hinge as the B₃ → B₄ Transition

At frequencies approaching 10⁸ Hz, signal propagation becomes limited by the speed of light rather than ionic diffusion. In DM terms, this is the ρ→Ψ boundary: the point where 3D local processes must transform into 4D wave-like propagation.

Mathematically, this corresponds to the embedding of B₃ into B₄, where an additional reflection axis (time-like) completes Lorentzian symmetry SO(1,3). Physically, it’s where local charge oscillations couple to coherent electromagnetic modes — the geometric precondition for wavefunction behavior. Thus, the neural lattice (B₃) connects to the wave lattice (B₄) at the 10⁸ Hz hinge, explaining why biological systems cannot exhibit sustained quantum coherence below this threshold.

7. Conscious Coupling in Standard Physics Terms

In standard language:
• Below 10⁸ Hz: signal processing is governed by electrochemical kinetics (diffusive, 3D, classical).
• Above 10⁸ Hz: electromagnetic coherence begins to dominate, introducing phase alignment, entanglement, and relativistic constraints.

Therefore, DM interprets consciousness as the interface regime where classical neural oscillations (B₃ symmetry) synchronize with the underlying electromagnetic field (B₄ symmetry). No exotic forces are invoked — only the geometric embedding of one symmetry into another.

In formal physics language, the “neural–consciousness hinge” around 10⁸ Hz corresponds to the transition from purely Euclidean B₃ symmetry (localized biological oscillations) to Lorentzian B₄ symmetry (propagating electromagnetic coherence), marking the minimal frequency at which 3D biological processes can couple coherently to 4D wave dynamics.

The DM framework unifies physics and human identity as geometry-driven information systems. Probabilities, randomness, and collapse are not fundamental mysteries but consequences of projection. The wavefunction is real, humans are stabilized coherence objects, and the universe itself is a nested geometric lattice transmitting information across scales.

"Face Value" Perspective

3D: Face of Cube = Point → Line → Square

Perspective is planar = All objects have planar surfaces = ρ Local, Classical

10⁶¹ (3D Observable Span): The ratio of the cosmic radius (10²⁶ m) to the Planck length (10⁻³⁵ m) represents the number of spatial Planck units filling the observable universe.

4D: Face of Tesseract = Line → Square → Cube

Perspective is a volume = All objects have volumetric surfaces = Ψ Quantum Wave

10¹²¹ (4D Tesseract Volume): Combining (10⁶¹) and (10⁶⁰) Planck ratios result in ~10¹²¹ Planck cells, defining the 4D tesseract volume.

5D: Face of Penteract = Square → Cube → Tesseract

Perspective is a hyper-volume = All objects have hyper-volumetric surfaces = Φ Coherence Field

10¹²² (5D Penteract Coherence): The jump from 10¹²¹ to 10¹²² represents the transition from 4D wave to 5D coherence, encompassing the full penteract structure.

The Simplest Langrangian

𝓛DM = (c⁴ / 16πG)(R + S) + 𝓛ρ + 𝓛Ψ + 𝓛Φ

Where:
R = Ricci scalar curvature of 4D tesseract volumes (Ψ).
S = Coherence curvature along the 5D s-axis, stabilizing Φ.
𝓛ρ = 3D localized energy on cube faces.
𝓛Ψ = 4D wavefunction propagation across tesseract volumes.
𝓛Φ = 5D coherence stability and dimensional projection.

The 5D coherence curvature S is defined as:

S = ∇ₛ² Φ - Λₛ e^{-s/λₛ}

This term governs the stabilization of 5D coherence surfaces, preventing singularities and ensuring smooth projection into 4D and 3D states. Λₛ represents the intrinsic curvature of the 5D penteract, while λₛ is the coherence length scale along s.

Einstein’s relativity governs 3D spacetime curvature (ρ), Schrödinger’s equation emerges as the 4D wave projection (Ψ), Maxwell’s equations describe 3D-embedded 4D wave motion, and Dirac’s formulation represents the first-order differential coupling across 4D–5D coherence boundaries. String theory and supersymmetry, rather than being separate frameworks, are geometric extrapolations of the same 5D structure, Φ(x, y, z, t, s). Each dimensional order encapsulates the preceding one as a boundary condition.

DM adds new physics not by discarding old models, but by showing they are boundary cases of higher-dimensional coherence geometry. This provides both mathematical closure and new predictive power.

⟂ 2D (Information Surfaces): Holographic principle, event horizons, and quantum information storage represent 2D surfaces encoding 3D data. Physical phenomena like the entropy–area relation (S = A / 4ℓₚ²) define these as lower-dimensional information boundaries.

ρ 3D (Relativity Domain): Classical and relativistic physics emerge here. Einstein’s field equations, Gμν = (8πG/c⁴)Tμν, define curvature as a function of energy density, capturing geometry’s 3D perception of 4D curvature. (3D surfaces encoding 4D data)

Ψ 4D (Quantum Mechanics): The wavefunction Ψ(x, y, z, t) operates as a volumetric coherence field, projecting 3D frames through time. Schrödinger and Dirac equations both arise as projections of the 5D coherence equation ∂Φ/∂s = (iħ/2m)∇²Φ. Relativistic corrections emerge as ρ ⇄ Ψ interface terms. (4D surfaces encoding 5D data)

Φ 5D (Coherence Field): Φ(x, y, z, t, s) represents the universal stabilization field, unifying electromagnetism, gravity, and quantum coherence. Here, String theory’s ten dimensions are reduced to a nested 5D penetrants symmetry (ten tesseracts). DM interprets each 'string vibration mode' as a geometric harmonic of the 5D coherence field.

Geometry defines reality. Every physical law is a direct result of geometric nesting.

Φ(x, y, z, t, s) → Ψ(x, y, z, t) → ρ(x, y, z) → ⟂(y, z)

Mass production begins at the Higgs (e.g., τ lepton, proton, neutron). Particles below this threshold (e.g., photons, neutrinos) do not collapse into mass, while those above this threshold gain mass.

10²³ Hz

10³³ Hz

650AA0D9-C921-4D33-BB2B-49A11D3D3475_edi

10⁴³ Hz

10²⁵ Hz

The speed of light (c) and the Planck frequency (1/tₚ) converge functionally at the Higgs field boundary. The speed of light is more than a physical limit — it is a geometric necessity arising from the structure of space-time. It serves as the bridge between the 3D velocity limit and the 4D wave-rate of the wavefunction.

Every transition from 3D localization to 4D wave propagation is paced by c

Mass (m) is a ‘stilled’ Ψ wave localized in ρ. Releasing that localization exposes the underlying wave energy; the conversion factor is c². Thus E = mc² expresses the geometric conversion between ρ-localized mass and Ψ wave energy at the universal projection rate.

• Classical (1–10⁸ Hz): localized / decoherent behavior.
• Relativity (10⁸–10²³ Hz): geometric causality and spacetime curvature.